iicaras

Mid-Side Separation

Separate

The problem

The goal is to find relations for a mid and a side channel for an audio signal from the left and the right channels, such that they for example can be separately processed. One way to view this problem is in terms of a vector space $W = \textup{span} (\hat{l}, \hat{r})$ with basis vectors $\hat{l}$ and $\hat{r}$ representing the left and right channels respectively. Let $\vec{w} \in W$ be the vector representation of an audio signal. Similarly, $\hat{s}, \hat{m} \in W$ represent the side and mid channels respectively. Then,

$$ \begin{aligned}

iicaras

Wavetables

🡪 iicaras

A wavetable refers to PCM sample data which contains single-cycle waveforms a wavetable synthesizer can select for it's oscillator [^def1][^def2]. Currently the most common container is a WAV file which includes a CLM chunk as defined by Steve Duda from Xfer Records [^xfer]. Another slightly less common format is the WT format from Surge XT [^Surge]. Both contain the same PCM data with different data chunks and support.

Creating Wavetables

Vital

iicaras

Harmonics

🡪 iicaras

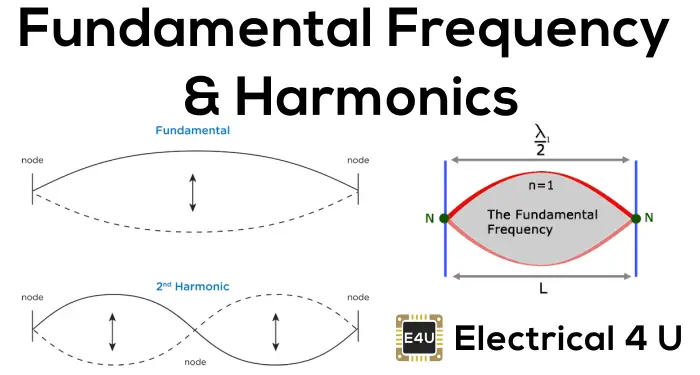
Image from Electrical4U [^harmonicsimage].

Harmonics can be understood from standing sine waves. A sine wave has 3 nodes. Therefore, the 'biggest' standing wave is the one where the first and second nodes define a constraining length $L$ such that half of its wavelength fits inside $L$. This is the fundamental. The second harmonic will have its entire wavelength fit inside $L$, since the end of the wavelength is now the node which sits at $L$. For the third harmonic, the next node is halfway through the second wavelength etc. Perhaps it is best visualised with a string. As such for wavelengths $\lambda_n$ with $n$ the harmonic number,

iicaras

Note Frequencies

🡪 iicaras

For a concert pitch of $\textup{A}_4 = 440 \textup{ hz}$, frequencies for each pitch in 12-TET are calculated using the equation

$$f_x = 2^{\tfrac{x}{12 \textup{ st}}}f_{\textup{A}_4},$$

with $[x] = \textup{ st}$ (semitones) and $x \in \mathbb{Z}$ [^harmonics]. The table below gives the frequency for each note between C0 and B10.