iq demodulation

iq_demod.py

import matplotlib.pyplot as plt
import numpy as np
from scipy import signal


# Source: https://github.com/guillaume-chevalier/filtering-stft-and-laplace-transform
def butter_lowpass_filter(data, cutoff_freq, sampling_freq, order=4):
    nyq_freq = 0.5 * sampling_freq
    normal_cutoff = float(cutoff_freq) / nyq_freq
    b, a = signal.butter(order, normal_cutoff, btype='lowpass')
    y = signal.filtfilt(b, a, data)
    return y
    

# helper, multiply with this to convert deg to rad    
rad = np.pi/180

# these are the parameters of our transmitted signal.
# a * np.cos(2*Pi*freq * t - phi)
phi = 45 * rad
a = 1
freq = 50


# this is the 'receiver' side, it needs to 'sample' the signal we are sending:
sampling_freq = 2000
t = np.linspace(0,1,sampling_freq)
omega = 2*np.pi*freq

signal_received = a * np.cos(omega * t - phi)

# we can also add some noise if we want:
# noise =  1 + 0.5 * np.random.uniform(-0.5, 0.5, sampling_freq)
# signal_received = signal_received * noise


# get i and q with a multuplication and a lowpass filteR:
signali = signal_received * np.sin(omega*t)
signali = butter_lowpass_filter(signali, freq, sampling_freq)

signalq = signal_received * np.cos(omega*t)
signalq = butter_lowpass_filter(signalq, freq, sampling_freq)


# we can get the amplitude back with this:
magnitude = 2 * np.sqrt(signali**2 + signalq**2)
plt.plot(magnitude, label="magnitude")

# we can get the 'angle' back with this:
freq = np.arctan2(signali, signalq)
plt.plot(freq / rad, label="angle")

plt.legend()
plt.show()

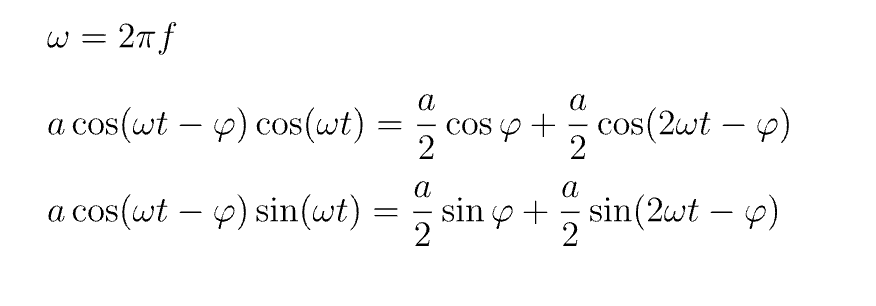
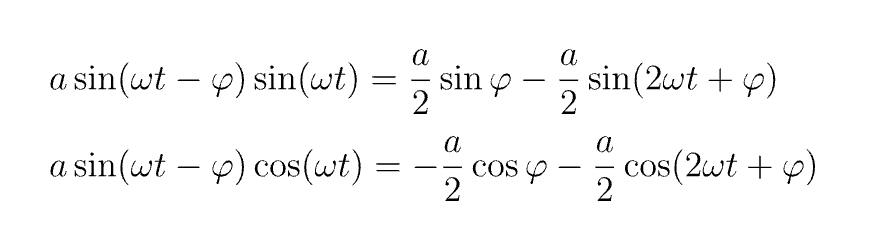
This is the schematics of an sdr, you can find the multiplication and filtering towards the output.

These are the equations I used, you can check them using the rules for sin(x+y) and cos(x+y)

two more for completeness:

Let's hope I didn't make a mistake somewhere.