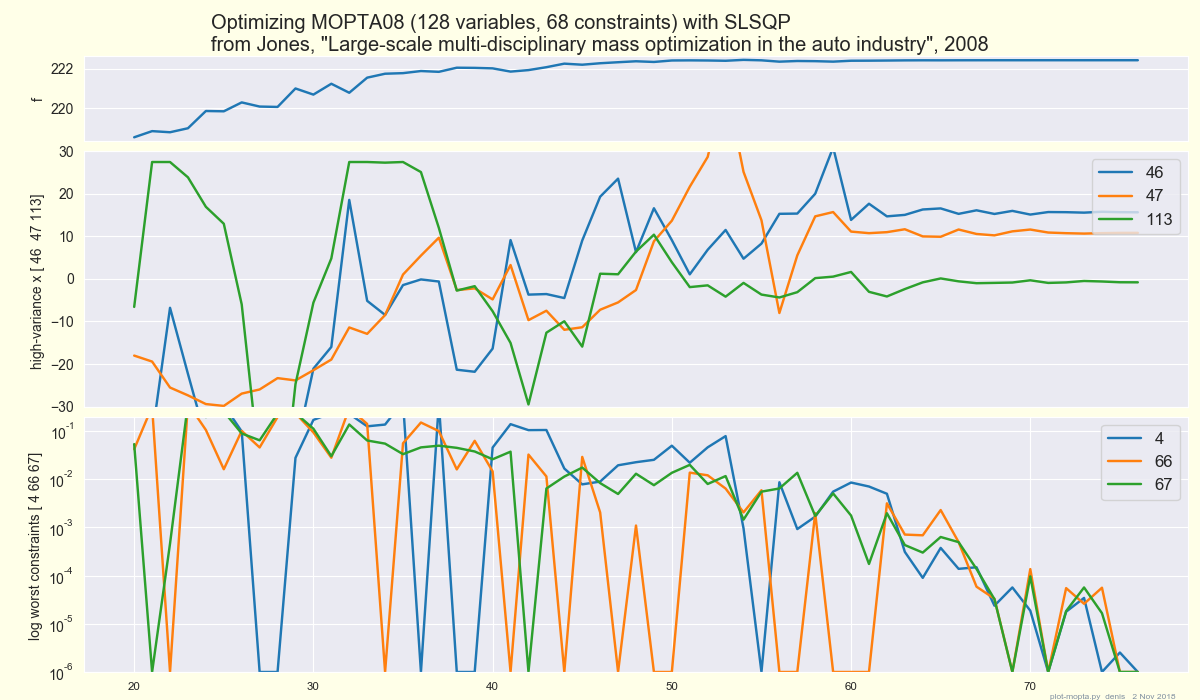
MOPTA08 is a test case for optimization from D.R. Jones, "Large-scale multi-disciplinary mass optimization in the auto industry" , 2008. It has 124 variables in 0 .. 1, a linear objective function, and 68 nonlinear constraints.
The purpose of mopta08-py is to try out various optimizers -> python -> MOPTA08,
10 years on, and see if we can learn anything.
Keywords: nonlinear optimization, benchmark, python, SLSQP, SQP, Sequential Quadratic Programming, MOPTA08.
1-slsqp-mopta.log: the log from a sample run.
f reaches 222.4 in < 100 iterations, ~ 20 minutes on an iMac.
mopta.py. Usage:
from mopta import func, gradf, constr, x0
f = func( x ) # the objective function, linear
grad = gradf( x ) # gradient, constant
cons = constr( x ) # 68 nonlinear constraints, that we want <= 0
x0 # from start.txt
N.B. python arrays are 0-origin -- py constraints 0 .. 67 are fortran 1 .. 68.
mopta-f2py: a shell script to compile *.f func.f90 funcpy.f90
and generate 2 macos dynamic libraries moptafunc.so libmopta.so, using f2py.
You'll have to change this for other platforms, and even on my mac 10.10
the dyld part is murky.
funcpy.f90: function func instead of subroutine, simplifies f2py
slsqp-mopta.py: runs the scipy SLSQP optimizer on mopta.
It uses datalogger to save f x constr at each iteration, to plot later.
(gist.github displays these in ascii order, hence leading 0- 1- in some filenames.)
The plot and logfile above show f -> its final value from below,
and violated constraints -> 0 from above, the "wrong side":
# iter sec func -df |dx|max constraints: nviol, sum, biggest 2
10 168 220.246 -2.3 dx 1 c 30 7.5 [2 0.6] [4 3]
20 327 218.52 -2.8 dx 0.77 c 26 1.6 [0.5 0.3] [4 3]
30 485 220.685 0.31 dx 0.35 c 26 1 [0.2 0.2] [4 3]
40 644 222.015 0.025 dx 0.17 c 23 0.22 [0.05 0.04] [4 3]
50 803 222.414 -0.075 dx 0.14 c 17 0.14 [0.05 0.02] [ 4 59]
60 962 222.402 -0.046 dx 0.17 c 15 0.019 [0.009 0.004] [4 3]
70 1121 222.427 6.6e-05 dx 0.0086 c 8 0.00048 [0.0001 0.0001] [66 59]
Are such "wrong side" methods good for other problems ? (Do interior-point methods care about "wrong side" at all ? Don't know.)
The original Fortran SLSQP is by Dieter Kraft, "A Software Package for Sequential Quadratic Programming", DFVLR-FB 88-28, 1988. Scipy.optimize wraps slsqp_optmz.f in slsqp.py.
See also:
Nocedal & Wright, Numerical Optimization,
chapter 18, Sequential Quadratic Programming pages 529 - 562.
Williams, SLSQP in fortran2008,
http://degenerateconic.com/slsqp and https://github.com/jacobwilliams/slsqp
(but f2py doesn't do fortran2008).
constr is called often (and it's quite slow, timeit ~ 120 ms):
number of calls of func, gradf, constr: [228, 77, 9855]
Almost all of these calls are I guess for finite-difference approximations
to the 68 x 124 Jacobian of constr(x).
Speedup, active set ? Plotting and scaling constraints must be more important.
A single problem, even one as good as MOPTA08, doesn't help us much in choosing a method for other problems. Is there a "zoo" of 5 or 10 real or realistic problems on the web, with data from complete runs ? Just as a real zoo helps zoology students learn about different kinds of animals, a "problem zoo" would help students of optimization.
We need not only a range of problems, but better ways of visualizing optimization paths in 100 dimensions — of making optimizers human-understandable.
cheers
— denis-bz-py at t-online dot de
Last change: 2018-11-03 Nov