The vital message to Romeo doesn't arrive in time because the plague is in town (so the messenger cannot leave Verona). Hearing from his servant that Juliet is dead, Romeo buys poison from an Apothecary in Mantua. He returns to Verona and goes to the tomb where he surprises and kills the mourning Paris. Romeo takes his poison and dies, while Juliet awakens from her drugged coma. She learns what has happened from Friar Laurence, but she refuses to leave the tomb and stabs herself. The Friar returns with the Prince, the Capulets, and Romeo's lately widowed father. The deaths of their children lead the families to make peace, and they promise to erect a monument in Romeo and Juliet's memory.
Romeo and Juliet are actually still alive, and managed to convince everyone that they did in fact, die. In secrecy, they go off to start a brand new life with each other. As they are frolicking away, Juliet starts getting tired from all that exercise, and asks Romeo to carry her. As Romeo says okay, he starts to realize that the next town over is actually a ways away! Romeo notices that if he were to make a grid of the area he is traversing through, the next town over would be at the bottom right of this grid, and he would be at the top left.
Given a grid of size "c" (columns) and "r" (rows), and the fact that Romeo carrying Juliet can only move down or right at any point in time, write a function that returns the number of possible unique paths there are to the next town over.
Note: Romeo knows for sure that the distance to the next town over (r or c) can't possibly be more than 100 (kilometers).
// Input: c = 3, r = 2
uniquePaths(3, 2) // should return 3 (grid of 2x3)
// right -> right -> down
// right -> down -> right
// down -> right -> right
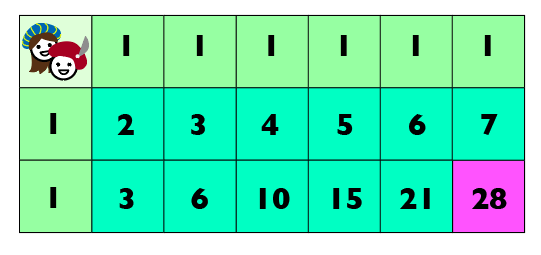
// Input: c = 7, r = 3
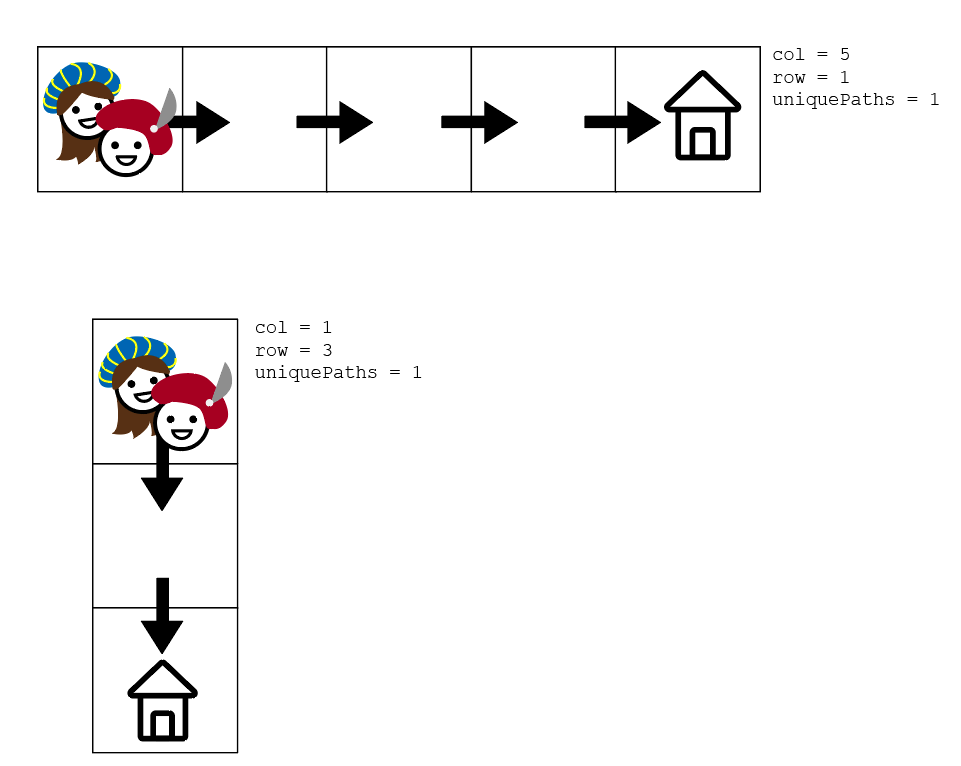
uniquePaths(7, 3); // should return 28Let's say that we only have one straight path, where c = 5 and r is 1:
The only unique path here will be the straight shot to the right, and the function whould return 1. The same goes for if c = 1, where our only path is a straight shot down. This will be our recursive base case.
In any other case, where c != 1 and r != 1, then what we can do is use recursion to go through every possible unique path, and slowly add those up.
function uniquePaths(c, r) {
if (c <= 1 || r <= 1) { // base case
return 1;
}
return uniquePaths(c - 1, r) + uniquePaths(c, r - 1);
}In hindsight, this solution works. However, the runtime here will end up being exponential O(2^c + 2^r) just like our recursive staircase problem. This is way too slow for Romeo to compute larger grid sizes! Not to mention that our space complexity here is also going to be O(A) where "A" is the depth of our recursive tree. (See picture below for what our recursive brances would look like.)
function uniquePaths(c, r) {
let paths = [];
for (let x = 0; x < c; x++) { // create a 2D array filled with null values.
let innerPath = [];
for (let y = 0; y < r; y++) {
innerPath.push(null);
}
paths.push(innerPath);
}
// replace each spot on the grid with the appropriate value, adding up from the neighboring values.
for (let i = 0; i < c; i++) {
for (let j = 0; j < r; j++) {
if (i === 0 || j === 0) {
paths[i][j] = 1;
} else {
paths[i][j] = paths[i - 1][j] + paths[i][j - 1];
}
}
}
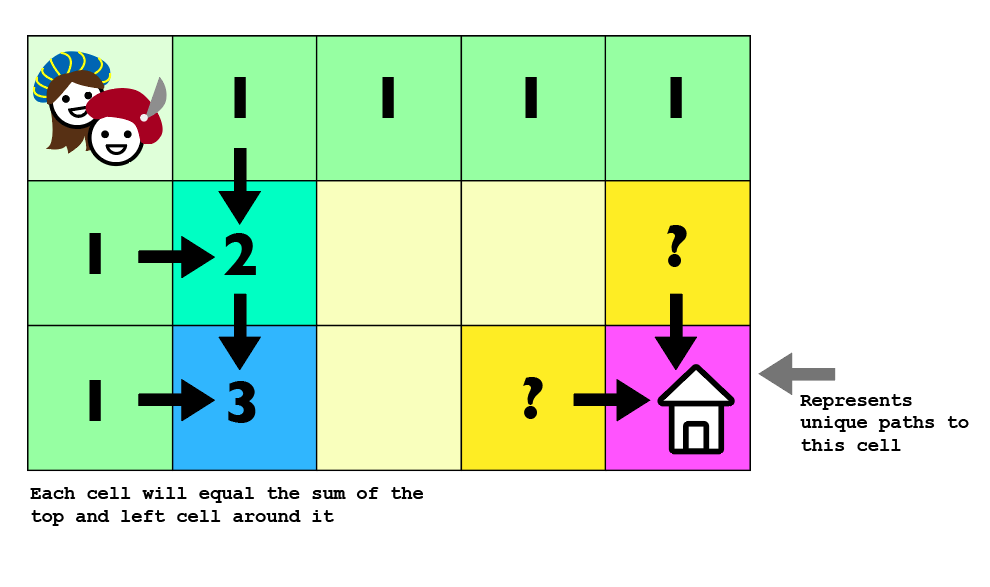
return paths[c - 1][r - 1]; // the value at the bottom right corner will equal the number of unique paths to this cell.
};This approach will add up the number of unique paths and store them in a cell in a grid. The number in each cell will represent the number of unique paths it takes to get to that specific cell, like so:
Using the idea behind the recursive solution, we can add up our values/unique paths and store them in a grid. This will allow us to dynamically go through whatever size grid we have and fill it up simply based off of neighboring values. This will cut the runtime down to O(c * r) where c is our columns (width of grid) and r is rows (height of grid). The space complexity directly correlates with the input size of our grid, and therefore takes up the same O(c * r) space. This is much better for Romeo to compute all his possible options in a shorter time frame. (He just needs a bit more space in his noggin to do so.)
To see the full story of Romeo and Juliet, go here: https://gist.github.com/cchoi34/1459758abba5be2c06d71bf3adf099c0