quantum_apps

quantum_apps.md

News

1. IBM 433Q
2. Atom Computing 1180 Q

Applications

Some evidence or verbal trick to illustrate the potential of quantum applications.

• Though in their infancy, the stability of qubits should become much better over time. -- IBM
• As IBM’s quantum hardware scales rapidly – from small prototype systems to more promising larger devices – researchers are excited about the possibility to one day handle previously insoluble routing problems.
• “A glimpse of the quantum future”
• As the hardware matures according to goals laid out in IBM Quantum’s hardware roadmap, the researchers expect to demonstrate a clear advantage over the classical competition.

VQA Basis

Parameter Shift

def shift_and_run(model, inputs, use_qiskit=False):
    param_list = []
    for param in model.parameters():
        param_list.append(param)
    grad_list = []
    for param in param_list:
        param.copy_(param + np.pi * 0.5)
        out1 = model(inputs, use_qiskit)
        param.copy_(param - np.pi)
        out2 = model(inputs, use_qiskit)
        param.copy_(param + np.pi * 0.5)
        grad = 0.5 * (out1 - out2)
        grad_list.append(grad)
    return model(inputs, use_qiskit), grad_list

Expectation

• k-commutativity and measurement reduction for expectation values, arXiv, 2023

Machine Learning

Refs

1. https://qiskit.org/textbook/ch-machine-learning/machine-learning-qiskit-pytorch.html#Contents
2. https://qulearn.baidu.com/textbook/chapter5/%E9%87%8F%E5%AD%90%E5%88%86%E7%B1%BB%E5%99%A8.html

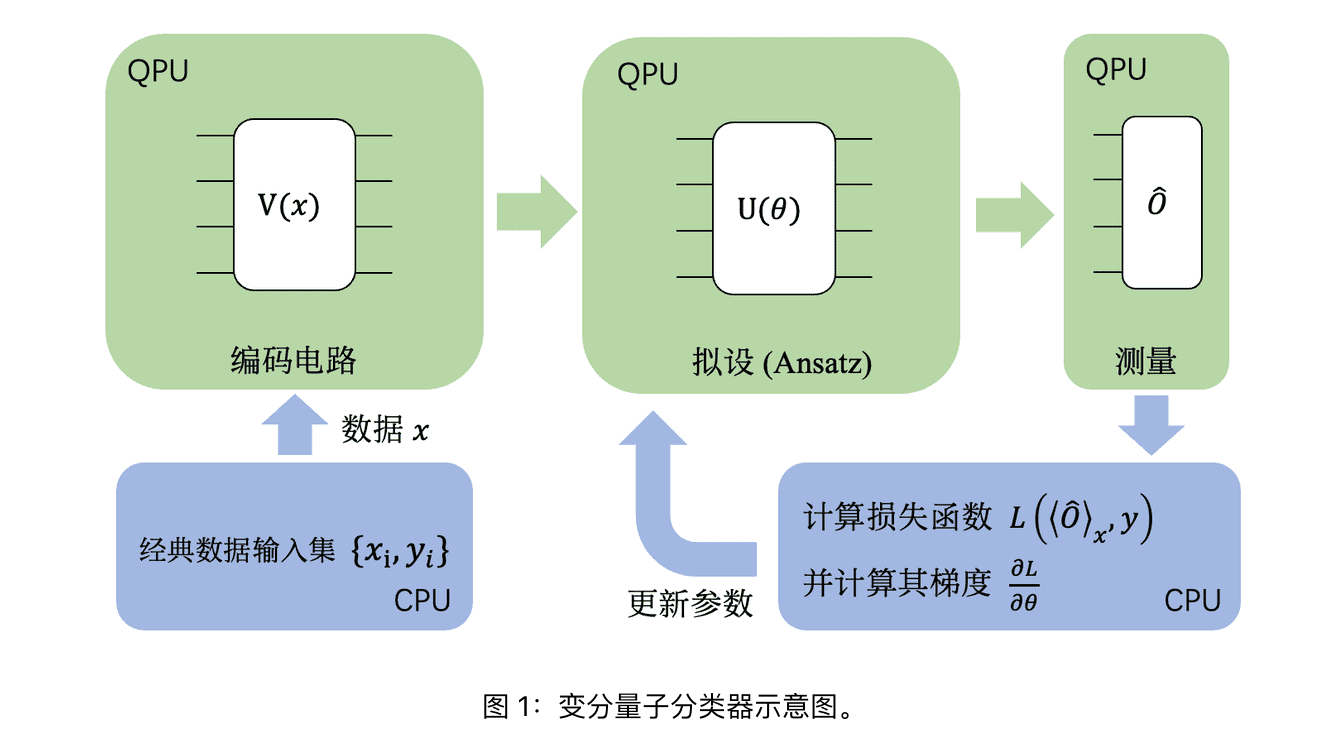
Brief

1. Classical data $\to$ quantum states (quantum data).
2. Quantum Variational Circuit (QPU)
3. Measure output and compute loss

Chemistry

Case: Quantum Chemistry with Qu&Co’s (now Pasqal) QUBEC on Amazon Braket

"To set expectations correctly, so far, no variational quantum algorithm has outperformed classical supercomputers in computational chemistry based on first principles (ab initio). However, recently quantum advantage has been demonstrated on a theoretical sampling task,[4] and an increasing number of academic and industrial works are bringing down the resource requirements, devising better quantum circuit strategies and more efficient optimization protocols. The race is on, and many believe chemistry or materials science applications to be one of the candidates to show early examples of industry relevant quantum advantage on near-term hardware."

Papers

• Evaluating the evidence for exponential quantum advantage in ground-state quantum chemistry (Nature-Comm 2023, CalTech)

Quantum Simulation

Reference: https://qml.baidu.com/tutorials/quantum-simulation/hamiltonian-simulation-with-product-formula.html

Utilize Product Formula To Simulate Time Evolution

According to one of the fundamental axioms of quantum mechanics, the evolution of a system over time can be described by $$ i\hbar\frac{\partial}{\partial t}|\psi\rangle = H|\psi\rangle $$ $\hbar$ is the reduced Planck constant. This equation is the well-known Schrödinger equation. Thus, for a time independent Hamiltonian, the time evolution equation of the system can be written as $$ |\psi(t)\rangle = U(t)|\psi(0)\rangle, U(t) = e^{-iHt} $$ Here we take the natural unit $\hbar = 1$ and $U(t)$ is the time evolution operator. The idea of simulating the time evolution process with quantum circuits is to approximate this time evolution operator using the unitary transformation constructed by quantum circuits.

Sample Question

For the Hamiltonian $H = I\otimes X + 0.5I\otimes Z - 0.2X\otimes X + 1.2Z\otimes I + 0.5Z\otimes Z$, find a quantum circuit $U$ to simulate $e^{-iH}$ with error tolerance 0.01 (i.e., $||U - e^{-iH}||\leq 0.01$). Moreover, try to use the idea of variational quantum circuit compiling to simplify the circuits.

Optimization

QAOA

• A Quantum Approximate Optimization Algorithm

Huawei

Intro from Huawei Mindspore

Google

qaoa-maxcut

IBM

qaoa

"It is important to say that, given the classical nature of combinatorial problems, exponential speedup in using quantum computers compared to the best classical algorithms is not guaranteed."

Baidu

Intro from Baidu

Combinatorial Optimization

Consists of $n$ bits and $m$ clauses. Each clause ( $C$ ) is a constraints for part of bits. Here $z$ represents the bit series $z_{1} z_{2} \dots z_{n}$

$$ C_j(z) = \begin{cases} 1 & \text{if clause $j$ is satisfied} \\ 0 & \text{if clause $j$ is not satisfied} \end{cases} $$

We have the objective function:

$$ C(z) = \sum_{j=1}^{m}{w_j C_j(z)} $$

Objective: find $z$ that maximize $C(z)$

Quantum Approximation Optimization Algorithm (QAOA)

"对于一个问题，如果我们找到了它的哈密顿量，根据这个哈密顿量我们可以求得它的本征态和本征能量，得到了本征态和本征能量就相当于解决了这个问题" -- 本源量子视频

Transform to an optimization problem on quantum system. Consider a compute basis $|z\rangle \in \lbrace0,1\rbrace^n$.

Define the Hamiltonian as:

$$ H_{C_j}|z\rangle = C_j(z)|z\rangle $$

Where the Hamiltonian can be constructed as:

$$ H_{C_j} = \sum_{z\in {0,1}^n}{C_j(z)|z\rangle \langle z|} $$

Why?

$$ \langle z'| z\rangle = \begin{cases} 1 & \text{if } z' = z \\ 0 & \text{else} \\ \end{cases} $$

So $\sum_{z'\in {0,1}^n}{C_j(z')|z'\rangle \langle z'|} z\rangle = C_j(z)|z\rangle$

For example, consider we have $z^{(1)}$ and $z^{(2)}$ that satisfy $C_j$, the the Hamiltonian is:

$$ H_{C_j}=|z^{(1)}\rangle \langle z^{(1)}|+| z^{(2)}\rangle \langle z^{(2)}| . $$

To this end, QAOA encodes the objective function $C$ into a $n$-Qubit quantum system's Hamiltonian.

$$ H_C=\sum_{j=1}^m w_j H_{C_j}, $$

Which satisfy the eigen equation:

$$ H_C|z\rangle=\sum_{j=1}^m w_j H_{C_j}|z\rangle=\sum_{j=1}^m w_j C_j(z)|z\rangle=C(z)|z\rangle $$

Notice that, assume the optimal solution is $z_{\text{opt}}$, we have:

$$ \left\langle z_{\mathrm{opt}}\left|H_C\right| z_{\mathrm{opt}}\right\rangle=\left\langle z_{\mathrm{opt}}\left|C\left(z_{\mathrm{opt}}\right)\right| z_{\mathrm{opt}}\right\rangle=C\left(z_{\mathrm{opt}}\right)\left\langle z_{\mathrm{opt}} \mid z_{\mathrm{opt}}\right\rangle=C\left(z_{\mathrm{opt}}\right) $$

Thus the optimal solution is the eigenvector of the Hamiltonian with the maximum eigenvalue ( $C_{max}$ )

For arbitrary quantum state $\psi$, we have:

$$ \langle \psi | H_C |\psi \rangle \leq C(z_{\text{opt}}) $$

Why? Because:

$$|\psi \rangle = \sum_i^n{c_i|z_i\rangle}, \sum_i^n{|c_i|^2} = 1$$

Therefore:

$$ \begin{aligned} \langle \psi | H_C |\psi \rangle &= \sum_{i}^{n}{c_i^* \langle z_i|} H_C \sum_{i}^{n}{c_i|z_i\rangle} \\ &= \sum_{i}^{n}{c_i^* \langle z_i|}\sum_{i}^{n}{c_i H_{C}|z_i\rangle} \\ &= \sum_{i}^{n}{c_i^* \langle z_i|}\sum_{i}^{n}{c_i C(z_i)|z_i\rangle} \\ &= \sum_{i}^{n}{C(z_i) c_i^*c_i \langle z_i|z_i \rangle} \\ &= \sum_{i}^{n}{|c_i|^2 C(z_i)} \\ &\leq \sum_{i}^{n}{|c_i|^2 C(z_{\text{opt}})} = C(z_{\text{opt}}) \end{aligned} $$

Max-cut Problem

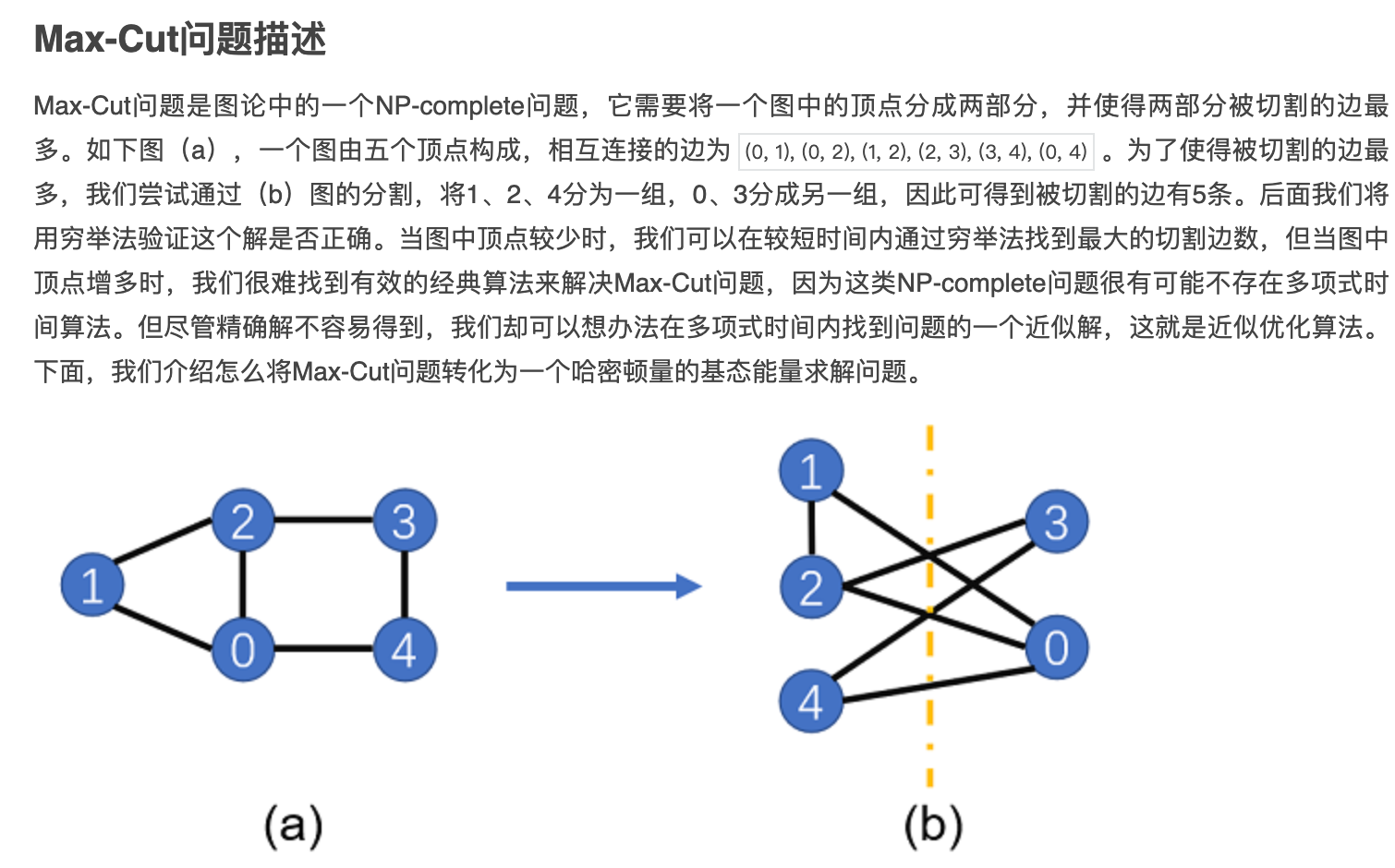
For a graph $G = (V,E)$, we have $n = |V|$ vertexes and $m = |E|$ edges. For each vertex $v$ in $G$, the value $z_v$ is 0 or 1 (0, 1 represent two partitions). For each edge $E = (u,v)$. A "clause" requires that $z_u \neq z_v$, meaning that vertex $v$ and $u$ are divided into different sub-sets. For each edge in the graph we have (XOR):

$$ C_(u,v)(z) = z_u + z_v - 2z_u z_v $$

Note that only $z_u \neq z_v$ results in 1, otherwise 0.

The entire problem is:

$$ C(z) = \sum_{(u,v)\in E}{C_(u,v)(z)}=\sum_{(u,v)\in E}{z_u + z_v - 2z_u z_v} $$

QAOA encoding

Hamiltonian $$ Z\equiv \begin{bmatrix} 1 & 0 \ 0 & -1 \end{bmatrix} \ Z|0\rangle = |0\rangle \ Z|1\rangle = -|1\rangle $$

Using $Z$ gate to construct Hamiltonian of the system. (Use mapping: $f(x)\rightarrow\frac{1-x}{2}$)

$$ \begin{aligned} H_C &= \sum_{(u,v)\in E}{C_(u,v)(z)} = \sum_{(u,v)\in E}{\frac{I-Z_u}{2} + \frac{I-Z_v}{2} - 2 \frac{I-Z_u}{2} \frac{I-Z_v}{2}} \\ &= \sum_{(u,v)\in E}{\frac{2I - Z_u - Z_v - (Z_u Z_v - Z_u - Z_v + I)}{2}} \\ &= \sum_{(u,v)\in E}{\frac{I - Z_u Z_v}{2}} \end{aligned} $$

---

Why? $$ \begin{aligned} H_C |z\rangle &= \sum_{(u,v)\in E}{\frac{I - Z_u Z_v}{2} |z\rangle} \ &= \sum_{(u,v)\in E}{\frac{|z_0\rangle \otimes \cdots \otimes (I - Z_u Z_v) |z_u z_v\rangle \otimes \cdots \otimes |z_n\rangle }{2}} \end{aligned} $$

Note that (according to equition 71):

$$ Z_u Z_v |z_u z_v\rangle = \begin{cases} -|z_u z_v\rangle & \text{if } z_u \neq z_v \\ |z_u z_v\rangle & \text{if } z_u = z_v \end{cases} $$

Here

$$ \begin{aligned} Z_u Z_v | z_u z_v \rangle &\equiv (Z_u \otimes Z_v) (z_u \otimes z_v) \\ &= Z_u|z_u\rangle \otimes Z_v|z_v\rangle \end{aligned} $$

Thus:

$$ \frac{|z_0\rangle \otimes \cdots \otimes (I - Z_u Z_v) |z_u z_v\rangle \otimes \cdots \otimes |z_n\rangle }{2} = \begin{cases} |z\rangle & \text{if } z_u \neq z_v \\ 0 & \text{if } z_u = z_v \end{cases} $$

Therefore

$$ \begin{aligned} H_C |z\rangle = \sum_{(u,v)\in E}{(z_u + z_v - 2z_u z_v)|z\rangle} \end{aligned} $$

---

The expectation of $H_C$ with state $\psi$ is: $$ \begin{aligned} \langle\psi|H_C| \psi\rangle &=\langle\psi|\sum_{(u, v) \in E} \frac{I-Z_u Z_v}{2}| \psi\rangle \ &=\langle\psi|\sum_{(u, v) \in E} \frac{I}{2}| \psi\rangle-\langle\psi|\sum_{(u, v) \in E} \frac{Z_u Z_v}{2}| \psi\rangle \ &=\frac{|E|}{2}-\frac{1}{2}\langle\psi|\sum_{(u, v) \in E} Z_u Z_v| \psi\rangle . \end{aligned} $$

Denote $H_D = -\sum_{(u, v) \in E} Z_u Z_v$, we need find $|\psi\rangle$ to maximize $\langle \psi| H_D | \psi \rangle$

How to construct the Quantum Circuit

$$ U_B\left(\beta_p\right) U_D\left(\gamma_p\right) \cdots U_B\left(\beta_1\right) U_D\left(\gamma_1\right), $$

Tune $\beta$ and $\gamma$ to find the optimal $| \psi (\beta, \gamma)\rangle$. The following figure is an implementation of $U_B(\beta)U_D(\gamma)$.

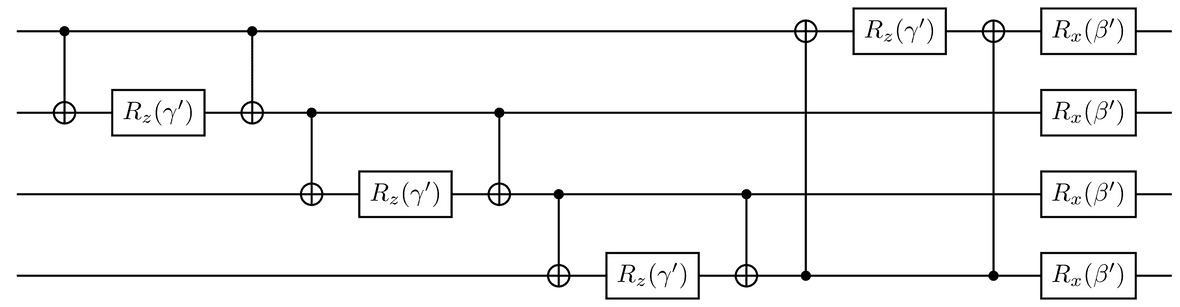
1. Construct the parameterized circuit.
2. Run the circuit to get output $\psi (\beta, \gamma)$.
3. Compute the cost function $C$ and optimize the parameters using classical optimizer.

The measurement results represent the solutions.

Summary

• Smaller expectation means more qubits connected by an edge have different quantum state, i.e., more edges have been cut.

• Why construct circuit like this?
• When computing loss function, is it still an exponential size problem?

VQA

Research Direction

Papers

(Bold font are to be summarized)

1. GraphQNTK: Quantum Neural Tangent Kernel for Graph Data, NIPS-2022
2. A rigorous and robust quantum speed-up in supervised machine learning, Nature-2021
   • Blog: https://research.ibm.com/publications/a-rigorous-and-robust-quantum-speed-up-in-supervised-machine-learning

System

• On-chip QNN: Towards Efficient On-Chip Training of Quantum Neural Networks, DAC-2022
• A Hybrid Deep Neural Network Architecture based on Quantum State Fidelity. MLSYS-2022
• A co-design framework of neural networks and quantum circuits towards quantum advantage, NC-2021
• FrozenQubits: Boosting Fidelity of QAOA by Skipping Hotspot Nodes, ASPLOS-2023
• RobustState: Boosting Fidelity of Quantum State Preparation via Noise-Aware Variational Training, Hanrui Wang, MIT.
• Combining Parameterized Pulses and Contextual Subspace for More Practical VQE. DAC. 2024
• Clapton: Clifford-Assisted Problem Transformation for Error Mitigation in Variational Quantum Algorithms. Fred Chong. 2024

AI

• Estimating the Density of States of Boolean Satisfiability Problems on Classical and Quantum Computing Platforms. AAAI-2020
• Learning to Optimize Variational Quantum Circuits to Solve Combinatorial Problems. AAAI-2020
• Revisiting Online Quantum State Learning. AAAI-2020
• Quantum Probabilistic Models Using Feynman Diagram Rules for Better Understanding the Information Diffusion Dynamics in Online Social Networks. AAAI-2020
• Quantum Cognitively Motivated Decision Fusion for Video Sentiment Analysis. AAAI-2021
• Variational Shadow Quantum Learning for Classification. AAAI-2021
• Sublinear Classical and Quantum Algorithms for General Matrix Games. AAAI-2021
• Quantum Exploration Algorithms for Multi-Armed Bandits. AAAI-2021
• Quantum-inspired Neural Network for Conversational Emotion Recognition. AAAI-2021
• A Quantum-inspired Complex-valued Representation for Encoding Sentiment Information (Student Abstract). AAAI-2021
• Quantum Binary Classification (Student Abstract). AAAI-2021
• Toward Physically Realizable Quantum Neural Networks. AAAI-2022
• Effective Multi-Class Classification on Quantum Computers Using an Ensemble of Diverse Quantum Classifiers. AAAI-2022
• Quantum Algorithms for Deep Convolutional Neural Networks. ICLR-2020
• Space-efficient Word Embeddings inspired by Quantum Entanglement. ICLR-2020
• Critical Points in Quantum Generative Models. ICLR-2022
• Sublinear quantum algorithms for training linear and kernel-based classifiers. ICML-2019
• Quantum Boosting. ICML-2020
• Quantum Expectation-Maximization for Gaussian mixture models. ICML-2020
• Reinforcement Learning for Molecular Design Guided by Quantum Mechanics. ICML-2020
• a Quantum Field Theory View of Deep Learning. ICML-2021
• Quantum algorithms for reinforcement learning with a generative model. ICML-2021
• Exponentially Many Local Minima in Quantum Neural Networks. ICML-2021
• Quantum-Inspired Algorithms from Randomized Numerical Linear Algebra. ICML-2022
• Equivariant Quantum Graph Circuits. ICML-2022
• Recurrent Quantum Neural Networks. NIPS-2020
• Exponential Speedup by Quantum Machine Learning without Sparsity and Low-Rank Assumptions. NIPS-2020
• Inductive Quantum Embedding. NIPS-2020
• The Inductive Bias of Quantum Kernels. NIPS-2021
• Reinforcement learning for optimization of variational quantum circuit architectures. NIPS-2021
• Private learning implies quantum stability. NIPS-2021
• Parametrized Quantum Policies for Reinforcement Learning. NIPS-2021
• A Hybrid Quantum-Classical Algorithm for Robust Fitting. CVPR-2022
• An Iterative Quantum Approach for Transformation Estimation from Point Sets. CVPR-2022
• Semiconductor Defect Detection by Hybrid Classical-Quantum Deep Learning. CVPR-2022
• Adiabatic Quantum Computing for Multi Object Tracking. CVPR-2022
• Tensor Network Based Efficient Quantum Data Loading of Images, IonQ-2023
• Symmetric Pruning in Quantum Neural Networks, ICLR-2023
• Quanvolutional Neural Networks: Powering Image Recognition with Quantum Circuits,
• Quantum Speedups for Zero-Sum Games via Improved Dynamic Gibbs Sampling. ICML-2023
• Q-Flow: Generative Modeling for Differential Equations of Open Quantum Dynamics with Normalizing Flows. ICML-2023
• Learning Distributions over Quantum Measurement Outcomes. ICML-2023
• Efficient Quantum Algorithms for Quantum Optimal Control. ICML-2023
• QAS-Bench: Rethinking Quantum Architecture Search and A Benchmark. ICML-2023
• Quantum Policy Gradient Algorithm with Optimized Action Decoding. ICML-2023
• A Hybrid Quantum-Classical Approach based on the Hadamard Transform for the Convolutional Layer. ICML-2023
• QuantumDARTS: Differentiable Quantum Architecture Search for Variational Quantum Algorithms. ICML-2023
• Near-Optimal Quantum Coreset Construction Algorithms for Clustering. ICML-2023
• Quantum Ridgelet Transform: Winning Lottery Ticket of Neural Networks with Quantum Computation. ICML-2023
• Quantum 3D Graph Learning with Applications to Molecule Embedding. ICML-2023
• Towards Quantum Machine Learning for Constrained Combinatorial Optimization: a Quantum QAP Solver. ICML-2023
• Analyzing Convergence in Quantum Neural Networks: Deviations from Neural Tangent Kernels. ICML-2023
• Efficient and Equivariant Graph Networks for Predicting Quantum Hamiltonian. ICML-2023
• Quantum Lower Bounds for Finding Stationary Points of Nonconvex Functions. ICML-2023
• Symmetric Pruning in Quantum Neural Networks. ICLR-2023
• QuAnt: Quantum Annealing with Learnt Couplings. ICLR-2023
• A Self-Attention Ansatz for Ab-initio Quantum Chemistry. ICLR-2023
• Classically Approximating Variational Quantum Machine Learning with Random Fourier Features. ICLR-2023
• Quantum Speedups of Optimizing Approximately Convex Functions with Applications to Logarithmic Regret Stochastic Convex Bandits. NIPS-2022
• Matrix Multiplicative Weights Updates in Quantum Zero-Sum Games: Conservation Laws & Recurrence. NIPS-2022
• Differentiable Analog Quantum Computing for Optimization and Control. NIPS-2022
• GraphQNTK: Quantum Neural Tangent Kernel for Graph Data. NIPS-2022
• Systematic improvement of neural network quantum states using Lanczos. NIPS-2022
• Escaping from the Barren Plateau via Gaussian Initializations in Deep Variational Quantum Circuits. NIPS-2022
• Concentration of Data Encoding in Parameterized Quantum Circuits. NIPS-2022
• Quantum Algorithms for Sampling Log-Concave Distributions and Estimating Normalizing Constants. NIPS-2022
• Power and limitations of single-qubit native quantum neural networks. NIPS-2022
• A Quantum-inspired Classical Algorithm for Separable Non-negative Matrix Factorization. IJCAI-2019
• Quantum-Inspired Interactive Networks for Conversational Sentiment Analysis. IJCAI-2019
• A Quantum-inspired Entropic Kernel for Multiple Financial Time Series Analysis. IJCAI-2020
• Solving Quantum-Inspired Perfect Matching Problems via Tutte-Theorem-Based Hybrid Boolean Constraints. IJCAI-2023

Misc

• Exponential Quantum Communication Advantage in Distributed Learning, Google, 2023
• Engineered dissipation to mitigate barren plateaus, IBM, 2023
• Quanvolutional Neural Networks: Powering Image Recognition with Quantum Circuits, Quantum Machine Intelligence, 2020
• Navigating the Dynamic Noise Landscape of Variational Quantum Algorithms with QISMET, ASPLOS, 2023
• RobustState: Boosting Fidelity of Quantum State Preparation via Noise-Aware Variational Training, Hanrui Wang, 2023

Basis

Encoding

ZZFeature-map

Quantum machine learning: development and evaluation of the Multiple Aggregator Quantum Algorithm

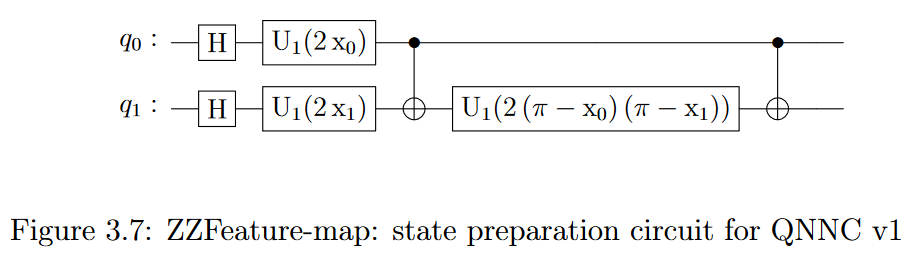
• Apply a Hadamard gate to each qubit, leaving it in a superposition.
• Apply $U_1(2x_0)$ gate to $|q_0\rangle$ and $U_1(2x_1)$ gate to $|q_1\rangle$.
• Apply a $cX$ gate with $|q_1\rangle$ as target and $|q_0\rangle$ as control.
• Apply a $U_1(\lambda)$ where $\lambda = 2(\pi - x_0)(\pi - x_1)$.
• Lastly, apply a $cX$ gate as in the second step.

Where $U_1(\lambda) = \begin{pmatrix} 1 & 0 \ 0 & e^{i\lambda} \end{pmatrix}$ , ${x_0,x_1}$ are two features that represent the input $x$.

• How to generate quantum kernel/operator, Lu Shun

amplitude encoding

https://pennylane.ai/qml/glossary/quantum_embedding

Circuit Design

QuantumFlow

A co-design framework of neural networks and quantum circuits towards quantum advantage, nature communication, 2021

Insight

Mapping specially designed neural network to quantum circuit.

Concentration of Data Encoding

• NIPS-2022

Key Insights

• The quantum divergence will concentrate to maximal mixed state with the depth increase.

Experiments

• On MNIST, downsample to $4\times 4$, encode using below angle encoding method, into $n$-qubit quantum states with encoding depth $D$, with $n\in {2,3,4,6,8}$ and $D\in {8,6,4,3,2}$ accordingly.
• Verify that with depth increase, accuracy decrease....

QuantumSEA

Key Insight Sparse topology (i.e., the way to prune gates?) changes each time the weights are updated.

RobustState

Motivation

• Parameter Shift ⇒ low training efficiency
• Simulator backpropogation ⇒ low robustness
• Solution: backpropogation on simulator, but using measurement from real machine

Clapton

Key Insight

• VQA can be transform to another equivalent VQA problem with different state search space, without affecting the final solution (energy).

LLM

References

1. https://thequantuminsider.com/2023/02/13/how-could-quantum-computing-improve-large-language-models/
2. https://medium.com/@thomasjmartin/quantum-computing-and-the-future-of-large-language-models-such-as-chatgpt-38de0028c462

QNLP Resources

1. https://cqcl.github.io/lambeq/examples/circuit.html (lambeq, transform sentence -> diagrams -> circuit )

Misc

Adiabatic Quantum Computing for Multi Object Tracking

Background

QUBO problem

Quadratic Unconstrained Binary Optimization

MOT

https://zhuanlan.zhihu.com/p/97449724

Steps

• Given a set of detections in each frame of a video, appearance features are extracted for each detection.
• By using a multi-layer Perceptron, pairwise appearance similarities between detections at different timesteps are computed
• Assign each detection to a track, such that the sum of the similarities of detections assigned to a single track is maximized.

What is the problem?

• Multi-Object Tracking is an NP-hard problem.

Quantum Vision Transformer

http://arxiv.org/abs/2209.08167

Background

Data loader for 1-dimensional vector

Definition:

Nearest centroid classification on a trapped ion quantum computer, NPJ Quantum

A data loader is a procedure that, given access to a classical data point $$ x = (x_1,x_2,\dots,x_d) \in \mathbb{R}^d $$ outputs a parametrized quantum circuit that prepares quantum states of the form $$ \frac{1}{||x||}\sum_{i=1}^d x_i|i\rangle $$

$d=8$-dimensional vector is encoded using 8 qubits?

There are 64 basis states: $|00000000\rangle,|00000001\rangle,\dots,|11111111\rangle$

Only 8 states: $|00000001\rangle, |00000010\rangle, \dots,|10000000\rangle$ are used.

QUANTUM DATA LOADERS FOR MATRICES

Give a matrix $X\in\mathbb{R}^{n\times d}$, we want to load it in a quantum state. $$ |X\rangle = \frac{1}{||X||} \sum_{i=1}^n \sum_{j=1}^d |e_i\rangle |e_j\rangle $$

QUANTUM ORTHOGONAL LAYERS

A quantum orthogonal layer is defined as a quantum circuit applied on a state $|x\rangle$ (encoded in the unary basis) to produce the output state $|Vx\rangle$. Where $V$ is the matrix corresponding to the unitary of the quantum orthonormal layer.

$$ RBS(\theta) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos \theta & \sin\theta & 0 \\ 0 & -\sin\theta & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} $$

Parameterised quantum circuits are specifically designed to learn the attention coefficients $$ A_{ij} = x_i^T W x_j $$ Three different approaches for implementing the quantum attention layer are introduced

QUANTUM ORTHOGONAL TRANSFORMER

1. Load $x_j$ into circuit using a vector loader
2. Apply a trainable quantum orthonormal layer $W$
3. Apply an inverse vector loader of $x_i$. Then the probability of measuring 1 on the first qubit is exactly $|x_i^TWx_j|^2=A_{ij}^2$.

---

$$ U|1\rangle = |x_i\rangle \to \langle 1|U^\dagger = \langle x_i| $$

$$ |1\rangle \langle 1| UWx_j = |1\rangle (\langle 1|U^\dagger)Wx_j = |1\rangle x_i^TWx_j $$

---

Comparison

Each classical attention layer requires $2d^2$ free parameters.

Quantum Convolutional Neural Networks

Related Work

• Quantum convolutional neural networks, Nature Physics, 2019
• Quanvolutional Neural Networks: Powering Image Recognition with Quantum Circuits, Quantum Machine Intelligence (Authors have run away...)

Dataset

QM7-X: https://arxiv.org/pdf/2006.15139.pdf

Ideas

Encoding

Encoding $2^n$-dimentional vector using $n$ qubits.

1. Construct unitary: see QC and QI exercise 2.7
2. Unitary synthesis -> encoding circuit.

On-chip Training

Nelder–Mead method