You're an industrious programmer that lives off the grid. The local well that you use to fetch water has gone dry, so you've decided to collect rain water to filter; however, your collection device isn't flat.
You are given an array of non-negative integers representing an elevation map of the collection device where the width of each bar is 1. Write a function that determines how much water the map is able to hold.
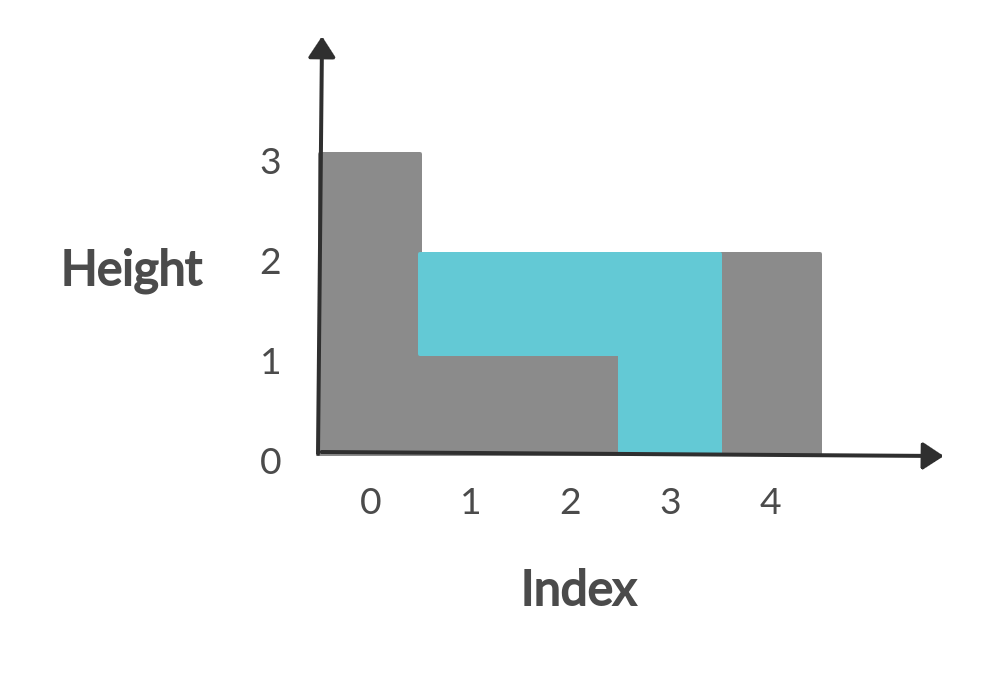
Given [0,1,0,2,1,0,1,3,2,1,2,1], return 6.
Visual Representation of above:
Here are some examples to test to be sure the function works. It is helpful to draw them out then walk step-by-step through the solution to help visualize it.
const heights = [0,1,0,2,1,0,1,3,2,1,2,1];
rainwaterCollector(heights) // return 6
const heights = [0,3,0,1,0,0,0,1,0,2];
rainwaterCollector(heights) // return 12
const heights = [0,5,3,2,8,8,1,1,2,4,3,3,7,1,2,4,3,2];
rainwaterCollector(heights) // return 38const heights = [3, 1, 1, 0, 2]
rainwaterCollector(heights) // returns 4const heights = [1, 5, 1, 0, 3, 1, 4, 0, 3]
rainwaterCollector(heights) // returns 14const heights = [2, 0, 4, 0, 0, 1, 0, 3, 0, 2, 0, 0, 6, 0, 5]
rainwaterCollector(heights) // returns 37-
This is definitely one of those problems where drawing it out and visualizing it helps. Make sure your interviewer is able to talk through the constraints of the heights inside of the device and how that might alter your resulting water. For Ex: If the walls from the beginning and end of the device are taller, the middle will generally be able to hold more water. Alternatively, if there is a tall wall and a short wall in between the device, that significantly diversifies how much water will "overflow" from where your highest height is from the shortest height you have and vice versa.
-
There are potential subproblems you can solve where you can calculate the separate water volume from each height - from beginning to the end. Ex: what is the volume from idx 0 - 1? What about from idx 1-2, etc. At each index point, there will be a specific volume of water it can hold.
-
The curr volume of water at every idx is the water height minus the minimum block height from previous blocks you've encountered from the left AND the right. What can you do to store or keep track of the water height in comparison to the previous heights? Answer: This is done by finding the max height from the left AND from the right. The MIN height from both sides will give you the max water volume BEFORE it overflows at that specific index. You then want to subtract that from the height its currently at and that will give you the total volume.
-
Have a var waterVolume to keep track of the total. If there is water at that specific index (whether you do horizontal or vertical approach), add it to its total.
-
You want to store the height of the max height from both sides inside of a DS, in this case, array(s). The max heights from the left AND right sides of the device will give you the minimum height needed to begin holding water. You need to figure out the most water at each point(the idx) of the device can hold given that there is a wall at the end - which will be the min height that can hold water minus the height of the block. If there isen't a block, then water overflows..
The water level at each index or height is determined by that block's largest leftwards neighbor, and it's largest rightwards neighbor. Each block has these "bounding walls". The water above each block will be the vertical distance between it and the smaller of these bounding walls.
We can loop through the array of heights in order to keep track of each block's largest leftwards neighbor. Then, we can run through them in reverse to determine each block's largest rightwards neighbor. Then we can do one final loop, where we determine the water above each block by subtracting its height from the smaller of its two bounding walls.
function rainwaterCollector (blocks) {
const rightMaxes = [];
let rightMax = 0;
for (let i = blocks.length - 1; i >= 0; i--) {
rightMax = Math.max(rightMax, blocks[i]);
rightMaxes[i] = rightMax;
}
const leftMaxes = [];
let leftMax = 0;
for (let i = 0; i < blocks.length; i++) {
leftMax = Math.max(leftMax, blocks[i]);
leftMaxes[i] = leftMax;
}
return blocks.reduce((waterCollected, block, idx) => {
const leftMax = leftMaxes[idx];
const rightMax = rightMaxes[idx];
return waterCollected + Math.min(leftMax, rightMax) - block;
}, 0);
}Time Complexity - O(3n) --> O(n) n - array.length. Space Complexity - O(2n) --> O(n) n - array.length.
You can simplify the above solution by merging the last two loops together — while keeping track of the leftwards maximum for any given block, we can also be calculating the water above it. This doesn't change anything in the grand scheme of things and may be SLIGHTLY faster but it may be harder to keep track of the moving variables.
function rainwaterCollector (blocks) {
const rightMaxes = [];
let rightMax = 0;
for (let i = blocks.length - 1; i >= 0; i--) {
rightMax = Math.max(rightMax, blocks[i]);
rightMaxes[i] = rightMax;
}
let waterCollected = 0;
let leftMax = 0;
for (let i = 0; i < blocks.length; i++) {
leftMax = Math.max(leftMax, blocks[i]);
const rightMax = rightMaxes[i];
waterCollected += Math.min(leftMax, rightMax) - blocks[i];
}
return waterCollected;
}Time Complexity - O(2n) --> O(n) n - array.length. Space Complexity - O(n) n - array.length.
Before we begin to sum the total water volume of the collector, it is important to use our understanding of water itself. Water will only gather up to the height of its reservoir walls. Therefore we should think about this problem in terms of height. Initially one might attempt to loop through the array and try to sum the volumes of the vertical columns of water. This approach quickly breaks down whenever the complexity of calculating the size of each reservoir is encountered.
Instead of summing the volume vertically we will think about how much volume exists in a horizontal plane at each incremental height. The solution below goes about this by starting at the highest 'peak' and and summing the total amount of volume at that level then decrementing the height by one and repeating the process until a height of 0 is reached. This produces an O(n*a) solution (n is the size of the array, a is the maximum number in the array). See individual comments to better understand the solution.
/* the 'totalVol' function will find the 'peak'
of the collection array then sum the volume
at each subsequent level util the 'ground'
is reached. */
function totalVol (blocks) {
// 'peak' is set to the return of Math.max()
// when it is applied to the array with
// 'null' as the 'this'.
const peak = Math.max(...blocks);
// instantiate volume to 0
let vol = 0;
// this loop starts at the 'peak' height
// then decrements the height
for (let height = peak; height > 0; height--) {
// 'peaksAtHeightLevel' is set to the return of
// 'peakIndicesMaker' which is an array of indices
// of reservoir walls that exist at that level.
const peaksAtHeightLevel = peakIndicesMaker(blocks, height);
// 'vol' is then incremented by the volume that exists
// at that level.
vol += volAtLevel(peaksAtHeightLevel);
}
// total volume is returned
return vol;
}
/* As demonstrated above this function takes
the original array as well as the height level
and returns an array of indices where reservoir
walls exist*/
function peakIndicesMaker (blocks, level) {
// instantiation
const peakIndices = [];
// loop over the entire array
for (let i = 0; i < blocks.length; i++) {
// if the wall height present at each index
// is at least the height of the given level
// then that index is pushed to the output array
if(blocks[i] >= level) {
peakIndices.push(i);
}
}
// array of indices is returned
return peakIndices;
}
/* This is the meat of the calculation for this problem.
The key point to understand is that the distance between
the two walls at the same height will also be the
volume of water held between them. Finally if two walls of
at least the same height are adjacent to one another then it
is not possible for water to be present.*/
function volAtLevel(peakIndices) {
// instantiation
let levelVol = 0;
// if there is only one wall at the height currently being
// calculated, there cannot physically be any water
// at that level. In this case we return 0 volume.
if(peakIndices.length === 1) {
return 0;
} else {
// If there is more than one wall of at least the current
// level being measured then the level volume is incremented
// for each 'pair' of walls at that level. It is important
// to note that we are comparing each wall to its adjacent
// neighbor located at the next index in the array. Therefore
// the last element in the array could not possibly hold water
// to its right. This is because no wall exists at that level
// beyond the last wall.
for (let i = 0; i < (peakIndices.length-1); i++) {
// this is the most important part of the function.
// Instead of simply summing the difference of the
// indices we have to think about the physical nature
// of the walls. The walls have a width of 1 so we
// need to measure the right side of one wall to the
// left side of its neighbor. This ensures that a total
// volume of 0 is added for adjacent walls.
levelVol += (peakIndices[i+1] - (peakIndices[i]+1));
};
}
// the level volume is then returned after all pairs have been summed.
return levelVol
}Time Complexity - O(n*h) n - array.length. h - max height. Space Complexity - O(n*h) n - array.length. h - max height.
We could refactor the same approach to more succinct recursive solution like so:
Time Complexity - O(n*h) n - array.length. h - max height. Space Complexity - O(n) n - recursive calls in the call stack.
function rainwaterCollector (height, level = Math.max(...heights)) {
if (level < 1) return 0;
let prevMatch;
const atThisLevel = heights.reduce((volOfWater, currHeight, idx) => {
if (currHeight < level) return volOfWater;
if (prevMatch) volOfWater += idx - prevMatch - 1;
prevMatch = idx;
return volOfWater;
}, 0);
return atThisLevel + rainwaterCollector(blocks, level - 1);
}#ShoutOutToJasmin
- Jasmin's gist gist
- Jasmin's Repl.it with lots of logging statements & solution code
- Jasmin's Solution 1 Slidedeck
- AlgoExpert under 'Water Area'
- Geeks for Geeks: Trapping Rain Water
- Leetcode: Trapping Rain Water